Limitations of ERC721A NFT and countermeasures using ERC721Psi
Soft Dev
21 Dec 2022
•
6 min read
I would like to share some gas fee related problems that I learned while carrying out the target project.
Due to the nature of the target, it was necessary to mint all tokens at once, so a NFT contract was created using ERC721A that supports batch mint and deployed to the mainnet.
How ERC721Psi Work
Recently, I just saw someone introduce the deformation related to ERC721. Among them, ERC721Psi is the most efficient one for reducing gas cost, so the idea of research arises. Here I would like to introduce to you the main improvements of ERC721Psi and how to improve them
Introduce ERC721
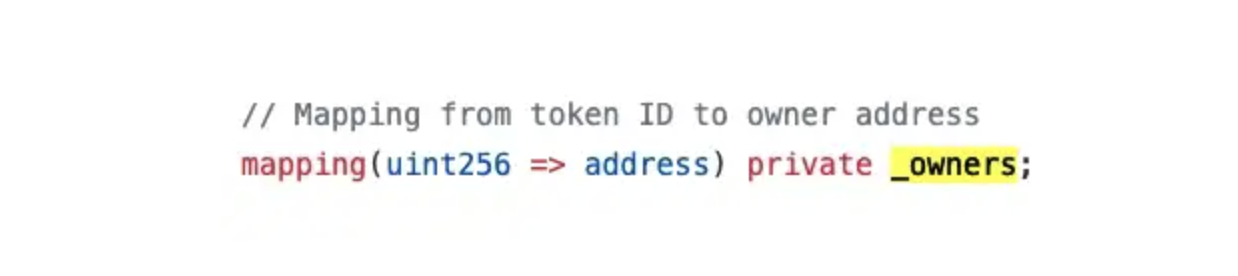
ERC721 is one of the current mainstream NFT formats (there is also ERC1155). Everyone's demand for NFT has increased, and the cost has followed. Various variants of ERC721 were born. Introduce some concepts of ERC721, these concepts help to understand how ERC721Psi reduces gas cost. In ERC721, each token corresponds to an NFT, and each token has its own tokenId sum owner. There will be _owners a to record tokenId the corresponding owner. When you send the token to others, you will modify _owners the token owner.
When you mint multiple NFTs at the same time, you need to write your address in the _owners corresponding position of these NFTs to indicate that you belong to these NFTs owner. This also leads to the fact that the gas required to spend mint with multiple NFTs will be multiple times that of mint with a single NFT. Is there any way to reduce the gas cost?
ERC721A
ERC721A was published by the well-known NFT Project — Azuki development team. Among them, the gas cost of mint multiple NFTs has been improved.
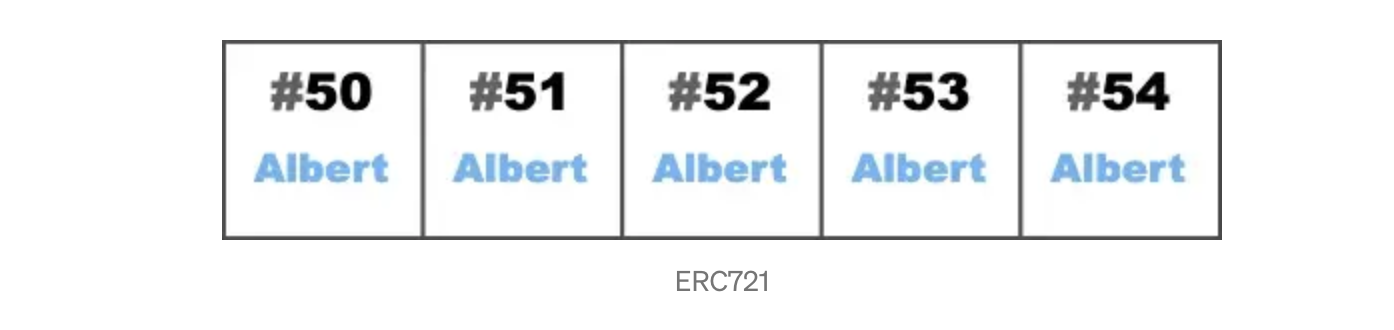
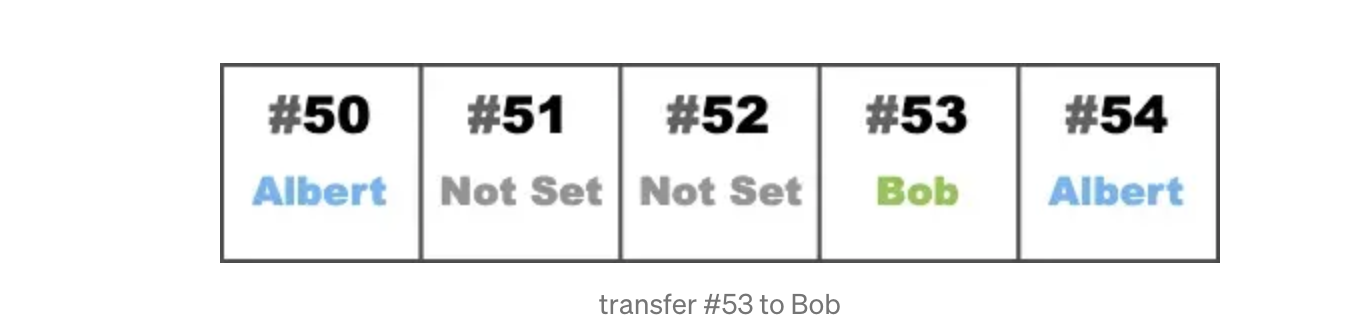
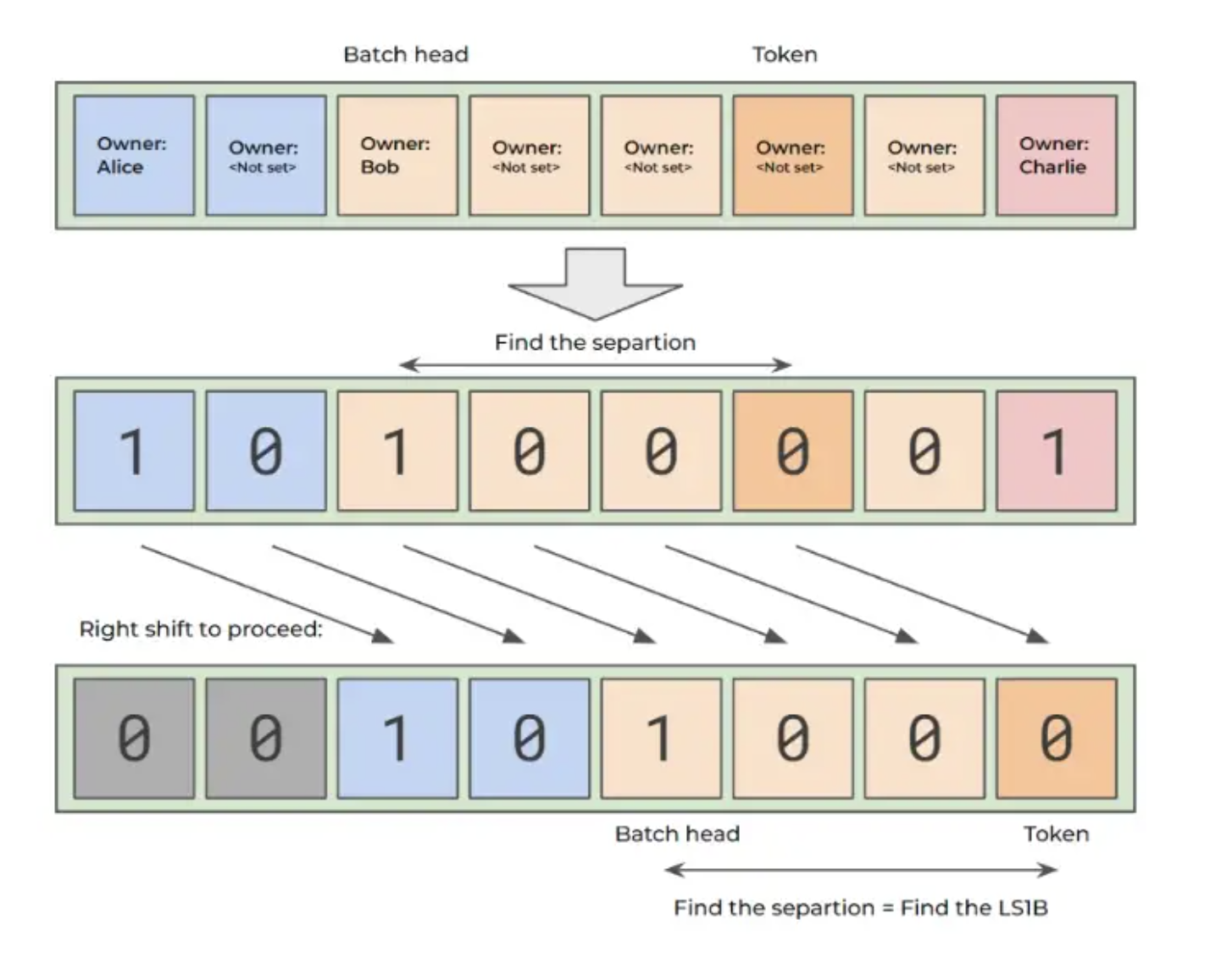
The principle I use an example to explain. Suppose today I (Albert) go to mint No. 50-No. 54 NFT (50,51,52,53,54) in one go. If it is the original ERC721 approach, the owner will be written as Albert in these NFTs.
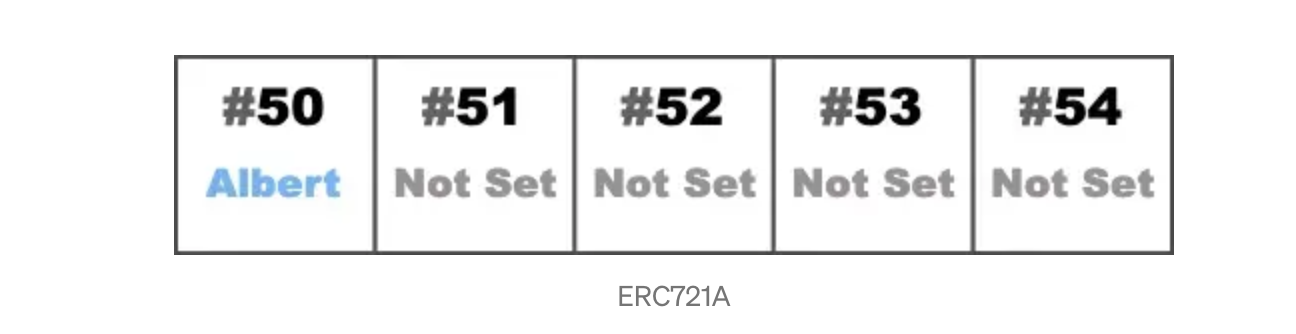
If the practice of ERC721A will change, only the first # 50) NFT will be filled with owner = Albert. Other NFTs # 51# 54) will be owner_not_set in the status of .
If we want to transfer# 53 NFT to Bob today, how do we know that the owner of# 53 NFT is Albert? At this point, we only need to look forward from# 53 NFT to find the first NFT with an owner, which is the owner of# 53 NFT. At this point, just fill in Bob as the owner of# 53 NFT, and fill in Albert as the owner of# 54 NFT. If the owner of# 54 NFT is not filled in with Albert, even# 54 NFT will be owned by Bob.
It can be seen from the figure above that from# 53 NFT to confirm that the owner is Albert, you need to find three tokens forward to know that the owner is Albert. Is there any way to know this quickly? This is the problem that ERC721Psi wants to improve.
ERC721Psi
ERC721Psi uses a magical algorithm to quickly locate the NFT with the owner closest to# 53. Before the explanation, there are some concepts that need to be explained to you first, so that you can know how to use it in ERC721psi later.
Bitmap
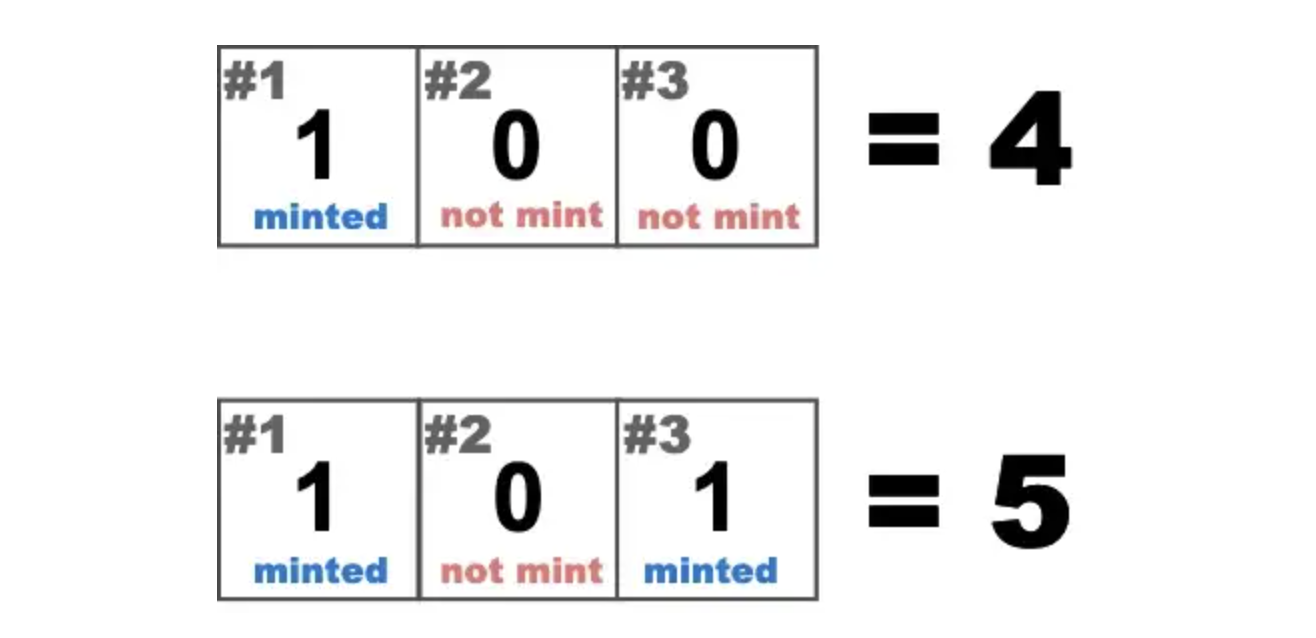
Because the data stored in the computer is stored in binary form, the binary characteristics are used to record and calculate data. Each of these bits can be used to record data individually. For example, there are three NFTs # 1,# 2 and# 3), we can use a uint8 variable with a bitmap to record whether they have been mint. Because the uint8 variable has exactly 3 bits ( 000) in binary representation. When each bit is 0, we can regard it as not being mint, and when the bit is , we 1can consider it has been mint out. The above picture shows that# 1 NFT has been released by mint, but# 2 and# 3 have not yet. At this time, the uint8 variable value is 4 (decimal). The uint8 variable is 5 (decimal), which means that both# 1 and# 3 are mint, but# 2 is not yet.
The Brown Sequence
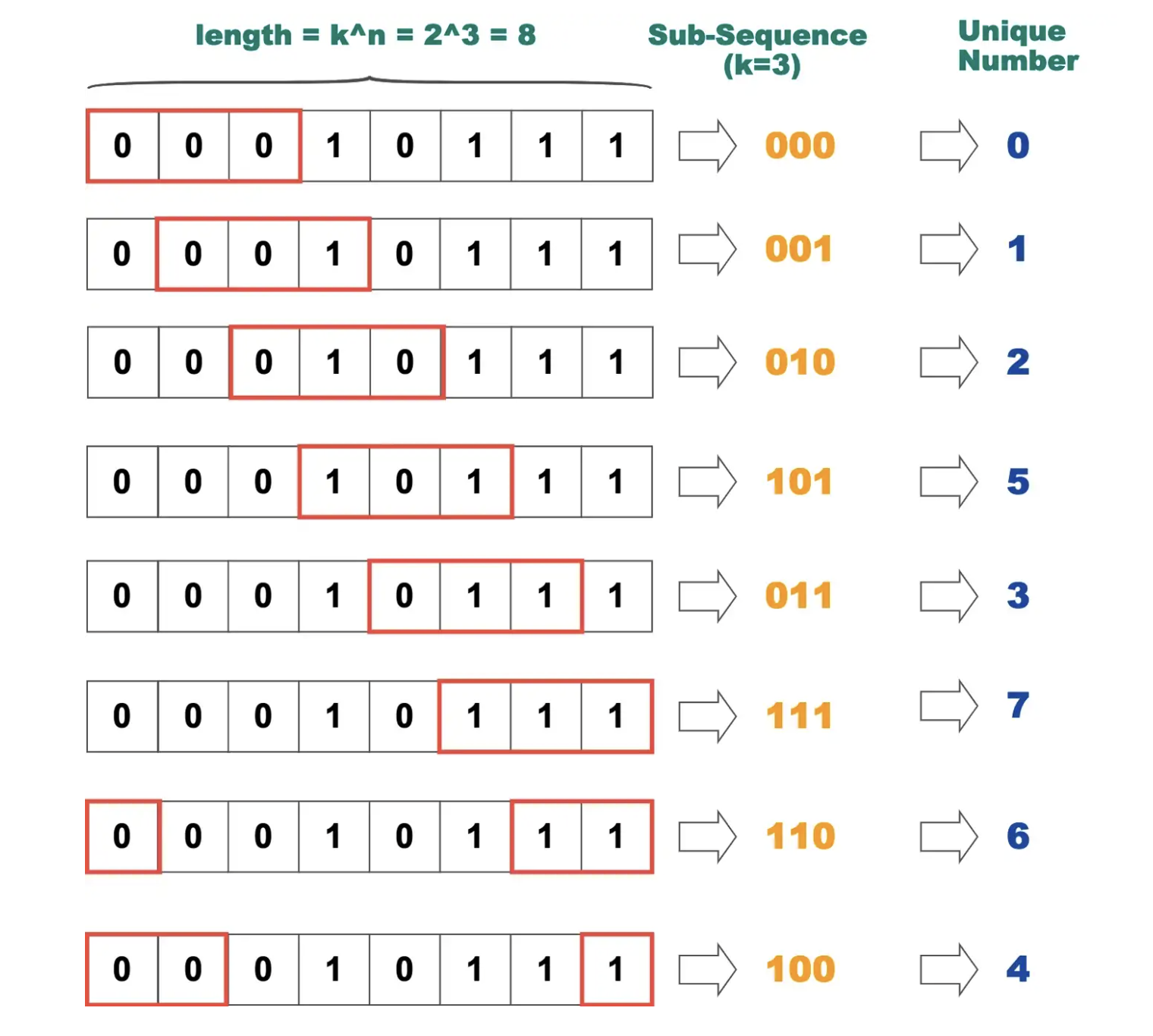
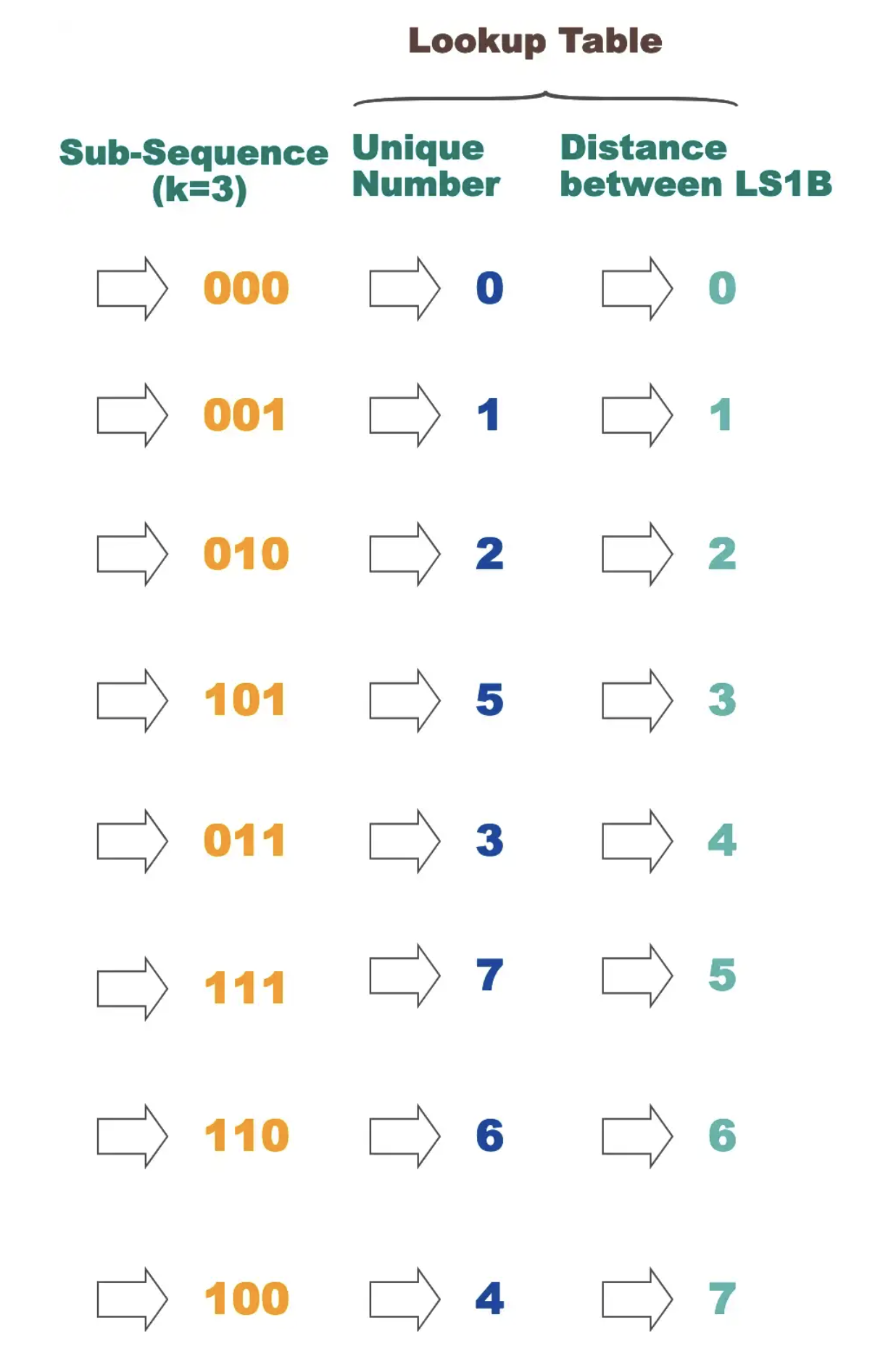
A de Bruijn sequence is a sequence of numbers with certain properties. When this sequence is composed of k kinds of letters, given a continuous sub-sequence of length n, the total length is k^n. The combinations in each sub-sequence are different, and we call this sequence a de Bruijn sequence (marked as B(k, n)). For example, if we set k=2, the letters will be represented by 0 and 1. n = 3: It means that the length of the continuous sub-sequence is 3. The entire sequence length will be 2³ = 8. The sequence 00010111 is just one of the de Brujin Sequences that meet these conditions. From the figure below, it can be found that each sub-sequence is a different permutation and combination. If you convert them into numbers, you will find that each sub-sequence will correspond to a unique number.
How to index the owner of token Id
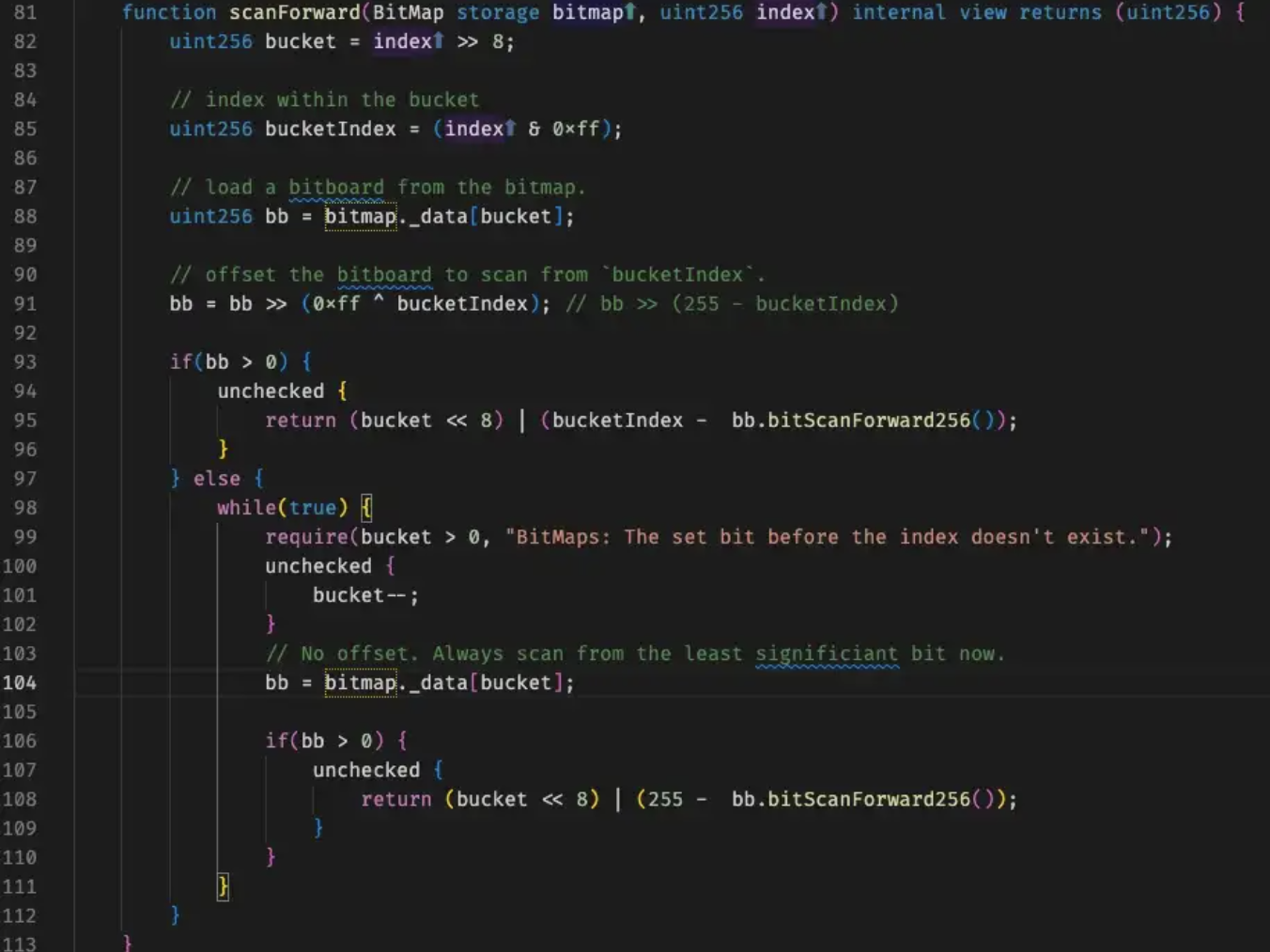
Use an example to illustrate how ERC721Psi uses the above two technologies to quickly find the owner. In the contract, 256 bitmap is used to record the owner. For the convenience of everyone's understanding, we still use 8 bitmap to illustrate. The main function BitMaps.sol is scanForward(uint256 index) ( index referring to tokenId).
Use Bitmap to record the existence of the owner of tokenId
uint256 bucketIndex = (index & off) Divide index by 256 to get the bucket where this tokenId will be placed. A bucket is 256 as a unit (representing the owner with 256 tokenIds stored). uint256 bucketIndex = (index & 0xff) Calculate the location corresponding to the tokenId in the bucket.
bb = bb >> (0xff ^ bucketIndex)
It is to move the bitmap corresponding to the tokenId to be queried to the far right. The situation will be as shown in the figure below. Batch Head is the owner of the tokenId we are looking for
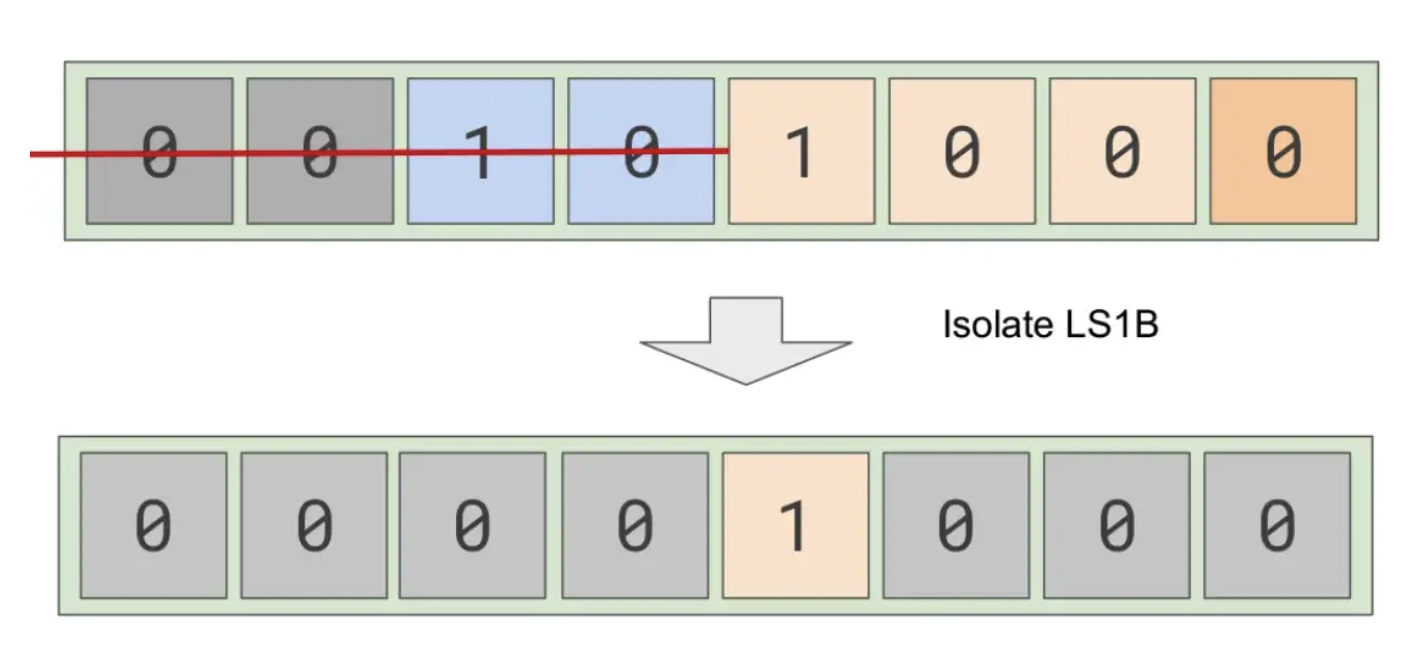
Find LS1B
We want the tokenId to stay where the first bit on the left is 1, and set the others to 0. A little trick is used here, as isolateLS1B256(uint256) shown in .
The second bit from the right bit equals 1 if bb = 6.
00000110 => 6
11111010 => -6
AND -------------
00000010
The rendered effect will be as shown in the figure below, except that the position of the first 1 from the right is 1, and the others are 0.
In the figure, it can be found that there are three intervals 1in the position of distance , so it means that we need to move to the right three times. So is there any way to know 1 ?
This will use the De Bruijn Sequence
Quickly find distance to LS1B using De Bruijn Sequence
De Bruijn Sequence takes the previous 000101111 as example. We now know that LS1B ( 00001000) is the fourth position from the right. At this time, multiplying LS1B ( 00001000) and De Bruijn Sequence( 000101111) is equivalent to shifting De Bruijn Sequence( 000101111) to the left by 4 bits. Then shift the result to the right by the number of k^n-ndigits (example k=2, n=3, 2^3-3 = 5). The corresponding and unique sub-sequence( 101) can be obtained.
000101111 => De Bruijn Sequence
000001000 => LS1B
* -------------
000101111000
// shift right 5 bit (k=2, n=3, 2^3-3=5)
000101111000 => 00000101 (only sub-sequence)
Because a unique sub-sequence will correspond to a unique number. We can build a map (or lookup table) for these numbers. The key is the sub-sequence number, and the value is the distance from LS1B. In this way, the distance to LS1B can be directly and quickly located without polling.
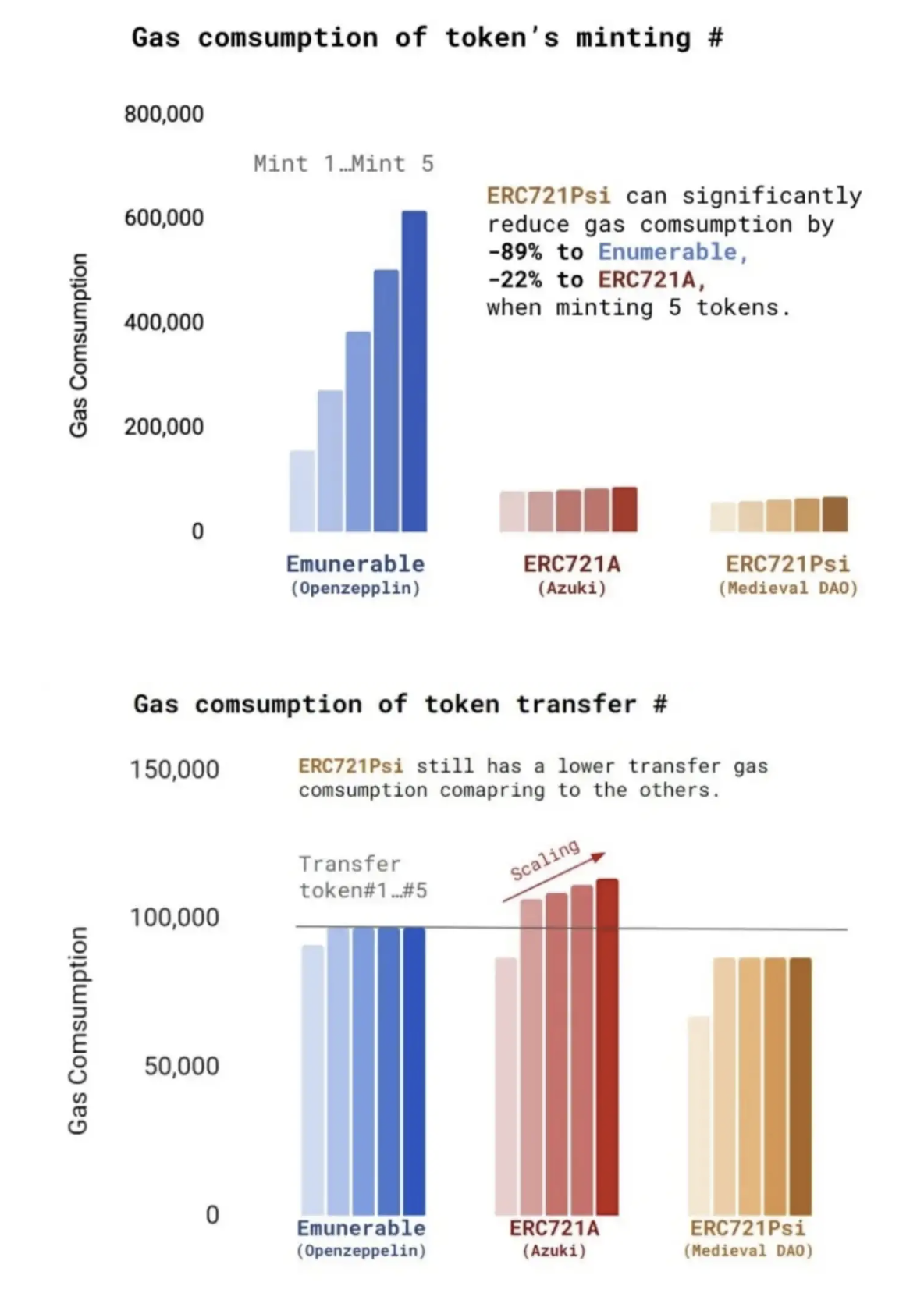
Gas Cost
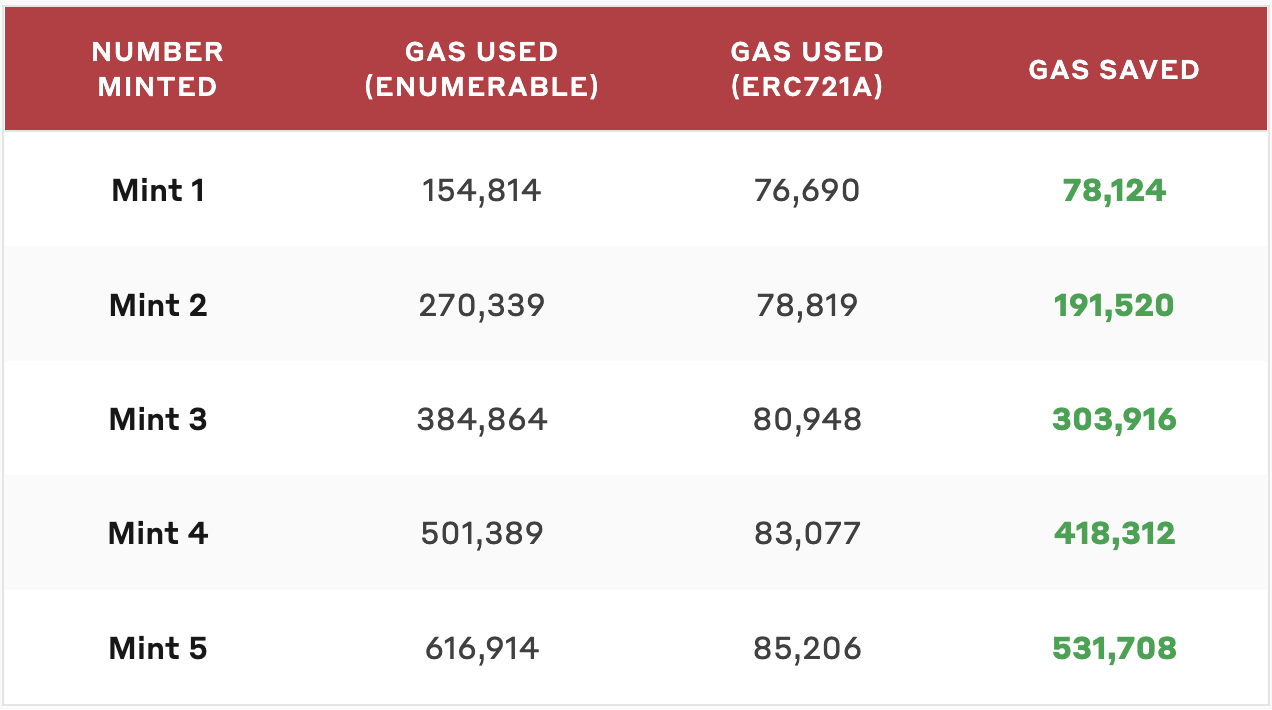
It can be found that the gas spent on executing mint or doing transfer has been significantly reduced.
Takeaway
The above are the main technologies used by ERC721Psi to reduce gas cost. The gas consumed by popular projects can be said to be very alarming. Therefore, when developing dApps at this stage, gas cost will also become one of the main considerations. The tricks used by the ERC721 Psi developers are ingenious and well worth learning. However, because ERC721Psi has not been verified by the market, whether it can guarantee certain security or not will take the test of time. With the rise of L2 or other L1 public chains, the gas cost has the opportunity to drop significantly. At that time, the architecture of dDapp will be further complicated and more functions can be realized!
Reference
Soft Dev
Senior Full-Stack Software Developer with 55+ repositories in various of skill sets on Backend, Web3 and Blockchain
See other articles by Soft
WorksHub
Jobs
Locations
Articles
Ground Floor, Verse Building, 18 Brunswick Place, London, N1 6DZ
108 E 16th Street, New York, NY 10003
Subscribe to our newsletter
Join over 111,000 others and get access to exclusive content, job opportunities and more!